LOLA refresher

LOLA requires comparing sets of intervals

Can we improve the efficiency to enable faster, larger-scale analysis?

If subject list has no containment, identifying overlaps is fast

The problem arises with contained interval overlaps

How can we improve efficiency without guaranteeing no containment?

Many approaches to solve the ‘containment’ issue:

• Nested Containment Lists (GRanges) (Alekseyenko and Lee, 2007; Aboyoun, P, Pages, H, and Lawrence, 2012)
• R-trees (bedtools) (Kent et al., 2002; Quinlan and Hall, 2010), Augmented interval trees (Cormen et al., 2001)

These methods try to structure the data to provide non-containment guarantees

Methods provide non-containment guarantees

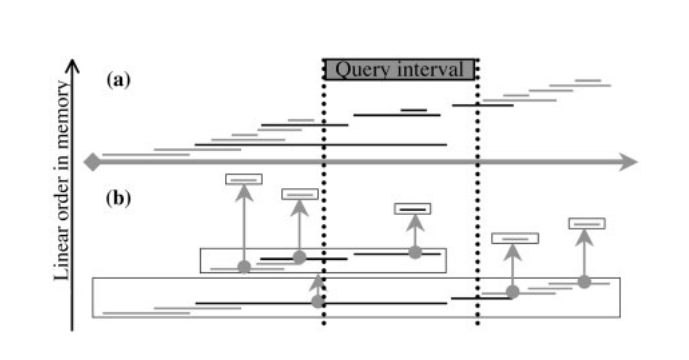
Augmented Interval List

1. Augment the list with the running maximum end value. solves the problem for lowly-contained lists

2. Decompose the list to minimize containment. extends the solution to highly-contained lists

Augment with the running maximum end value, maxE

Provides a local guarantee of no containment.

AIList works on contained lists

But long containment runs are problematic

Decompose long runs with constant maxE

Performance

• How does the maxE minimum run length affect performance?
• How does it compare to existing approaches?
• How does it scale with increasing size of subject?

Datasets

How does the maxE minimum run length affect performance?

How does it compare to existing approaches?

How does it scale with increasing size of subject?

Conclusion and Directions