Computational methods for region-based analysis of epigenome signals

Nathan Sheffield, PhD

www.databio.org/slides

outline

The (epi)genome revolution

Epigenome tools

20%

40%

Project organization

◁ Questions ▷

The genome revolution

A revolution driven by DNA sequencing technology

Sequencing technology can also measure epigenome signals

Epigenomics is the study of the chemical modification and physical conformation of cellular DNA and bound proteins

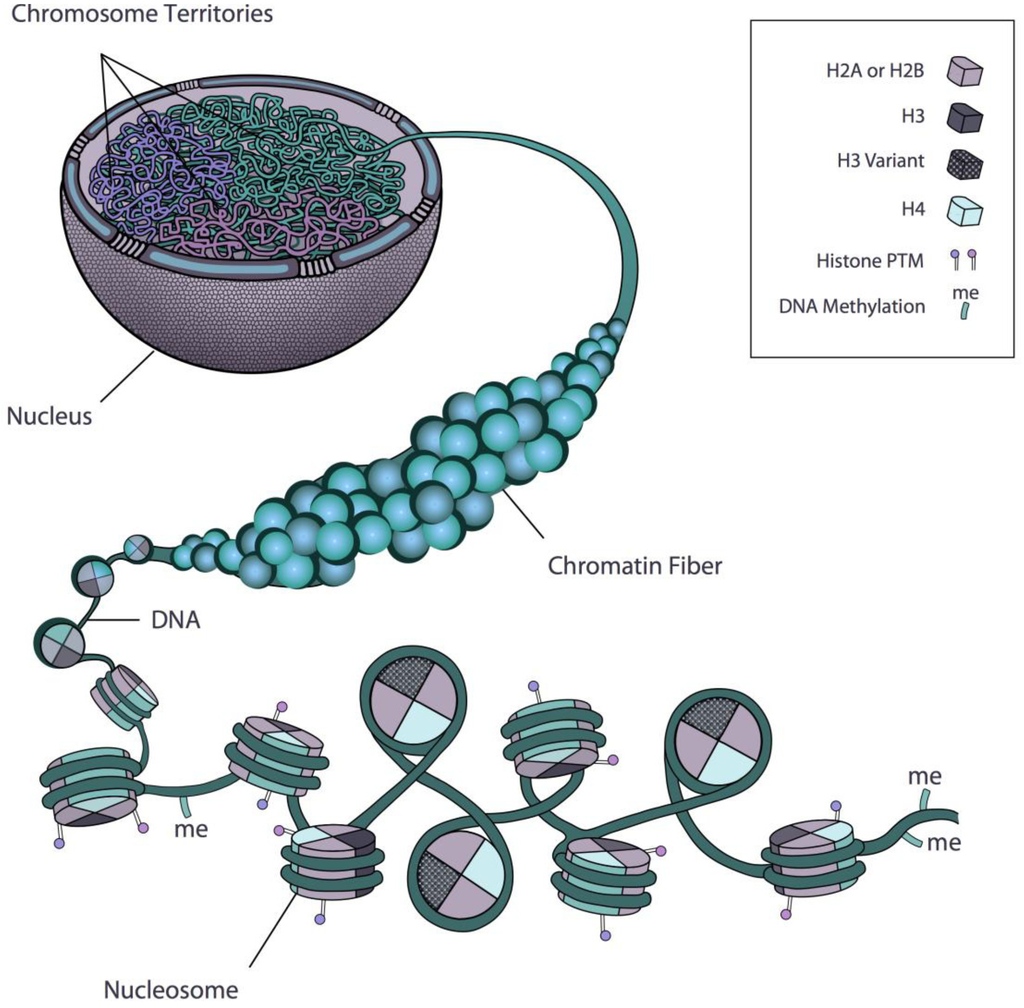
Rosa et al. 2013

Histone modification:
ChIP-seq
DNA methylation:
Bisulfite-seq
Chromatin accessibility:
ATAC-seq

The Sequence Read Archive is growing

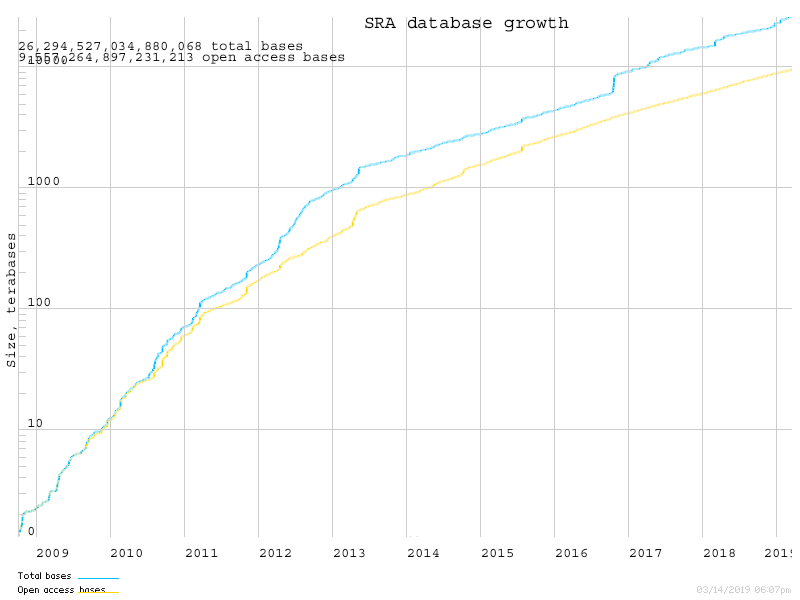https://www.ncbi.nlm.nih.gov/sra/docs/sragrowth/

Data is becoming more...

abundant

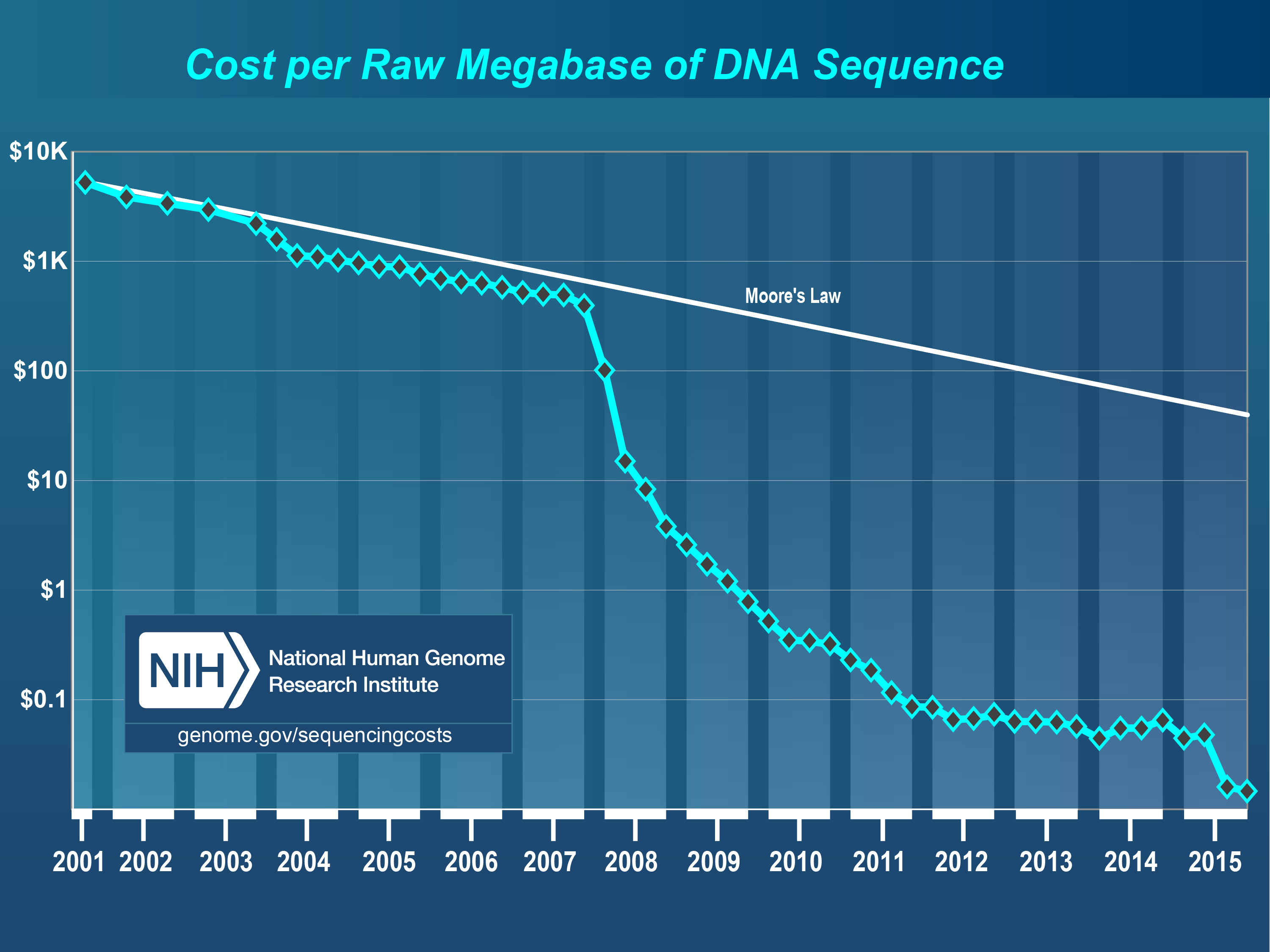
available

powerful

So why are the world's problems not solved?

First step in bioinformatics analysis:

pipeline

Papers with
"bioinformatics pipeline"
in title

Problem solved?

Data munging

Then, downstream tools need a different organization

What if?

Microwave syndrome

In user interface design, prioritizing easy access to integrated functions over their individual components.

The UNIX philosophy

[T]he power of a system comes more from the relationships among programs than from the programs themselves.

Many UNIX programs do quite trivial tasks in isolation, but, combined with other programs, become general and useful tools.

- Kernighan and Pike, The UNIX Programming Environment (1983, p. viii)

Problem

Solution

Problem

Solution

PEP: Portable Encapsulated Projects

PEP format

Start with a simple CSV with tabular data.

samples.csv

sample_name,protocol,organism,input_file
frog_0h,RNA-seq,frog,/path/to/frog0.gz
frog_1h,RNA-seq,frog,/path/to/frog1.gz
frog_2h,RNA-seq,frog,/path/to/frog2.gz
frog_3h,RNA-seq,frog,/path/to/frog3.gz

PEP format

Add a YAML for project-level data.

samples.csv

sample_name,protocol,organism,input_file
frog_0h,RNA-seq,frog,/path/to/frog0.gz
frog_1h,RNA-seq,frog,/path/to/frog1.gz
frog_2h,RNA-seq,frog,/path/to/frog2.gz
frog_3h,RNA-seq,frog,/path/to/frog3.gz

project_config.yaml

sample_table: /path/to/samples.csv
output_dir: /path/to/output/folder
other_variable: value

Add programmatic sample and project modifiers.

Derived attributes

Implied attributes

Subprojects

Derived attributes

Automatically build new sample attributes from existing attributes.

Without derived attribute:



| sample_name   | t    | protocol        | organism | input_file             |
| ------------- | ---- | :-------------: | -------- | ---------------------- |
| frog_0h       | 0    | RNA-seq         | frog     | /path/to/frog0.gz      |
| frog_1h       | 1    | RNA-seq         | frog     | /path/to/frog1.gz      |
| frog_2h       | 2    | RNA-seq         | frog     | /path/to/frog2.gz      |
| frog_3h       | 3    | RNA-seq         | frog     | /path/to/frog3.gz      |

Using derived attribute:



| sample_name   | t    | protocol        | organism | input_file             |
| ------------- | ---- | :-------------: | -------- | ---------------------- |
| frog_0h       | 0    | RNA-seq         | frog     | my_samples             |
| frog_1h       | 1    | RNA-seq         | frog     | my_samples             |
| frog_2h       | 2    | RNA-seq         | frog     | my_samples             |
| frog_3h       | 3    | RNA-seq         | frog     | my_samples             |
| crab_0h       | 0    | RNA-seq         | crab     | your_samples           |
| crab_3h       | 3    | RNA-seq         | crab     | your_samples           |



| sample_name   | t    | protocol        | organism | input_file             |
| ------------- | ---- | :-------------: | -------- | ---------------------- |
| frog_0h       | 0    | RNA-seq         | frog     | my_samples             |
| frog_1h       | 1    | RNA-seq         | frog     | my_samples             |
| frog_2h       | 2    | RNA-seq         | frog     | my_samples             |
| frog_3h       | 3    | RNA-seq         | frog     | my_samples             |
| crab_0h       | 0    | RNA-seq         | crab     | your_samples           |
| crab_3h       | 3    | RNA-seq         | crab     | your_samples           |

Project config file:

sample_modifiers:
  derive:
    attributes: [input_file]
    sources:
      my_samples: "/path/to/my/samples/{organism}_{t}h.gz"
      your_samples: "/path/to/your/samples/{organism}_{t}h.gz"

{variable} identifies sample annotation columns

Benefit: Enables distributed files, portability

Implied attributes

Add new sample attributes conditioned on values of existing attributes

Before:



| sample_name   | protocol        | organism | 
| ------------- | :-------------: | -------- | 
| human_1       | RNA-seq         | human    | 
| human_2       | RNA-seq         | human    | 
| human_3       | RNA-seq         | human    | 
| mouse_1       | RNA-seq         | mouse    |

After:



| sample_name   | protocol        | organism | genome | 
| ------------- | :-------------: | -------- | ------ |
| human_1       | RNA-seq         | human    | hg38   |
| human_2       | RNA-seq         | human    | hg38   |
| human_3       | RNA-seq         | human    | hg38   |
| mouse_1       | RNA-seq         | mouse    | mm10   |



| sample_name   | protocol        | organism | 
| ------------- | :-------------: | -------- | 
| human_1       | RNA-seq         | human    | 
| human_2       | RNA-seq         | human    | 
| human_3       | RNA-seq         | human    | 
| mouse_1       | RNA-seq         | mouse    |

Project config file:

sample_modifiers:
  imply:
    - if: 
        organism: human
      then:
        genome: hg38
    - if:
        organism: mouse
      then:
        genome: mm10

Benefit: Divides project from sample metadata

Subprojects

Define activatable project attributes.

project_modifiers:
  amendments:
    diverse:
      metadata:
        sample_annotation: psa_rrbs_diverse.csv
    cancer:
      metadata:
        sample_annotation: psa_rrbs_intracancer.csv

Benefit: Defines multiple similar projects in a single file

Locus Overlap Analysis

http://code.databio.org/LOLA/

Sheffield and Bock (2016). Bioinformatics.

Nagraj, Magee, and Sheffield (2018). Nucleic Acids Research.

If subject list has no containment,
identifying overlaps is fast

binary search on start intervals, followed by backward steps:

The problem arises with contained interval overlaps

How can we improve efficiency
without guaranteeing no containment?

Many approaches to solve the 'containment' issue:

- Nested Containment Lists (GRanges) [@Alekseyenko2007; @Aboyoun2012] - R-trees (bedtools) [@Kent2002; @Quinlan2010], Augmented interval trees [@Cormen2001] These methods try to structure the data to provide non-containment guarantees

Methods provide non-containment guarantees

R-trees

Annotates tree nodes with a minimum bounding rectangle of elements. A query that does not intersect the bounding rectangle will not intersect any child element.

Nested Containment Lists

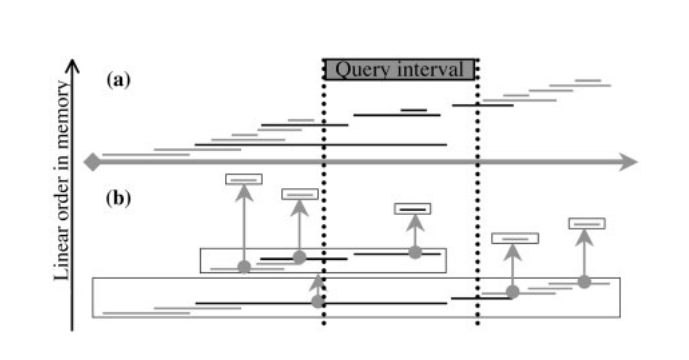
Augmented Interval List

1. Augment the list with the running maximum *end* value. *solves the problem for lowly-contained lists* 2. Decompose the list to minimize containment. *extends the solution to highly-contained lists*

Augment with the running maximum end value, `maxE`

Provides a local guarantee of no containment.

AIList works on contained lists

But long containment runs are problematic

Decompose long runs with constant `maxE`

Performance

How does the `maxE` minimum run length affect performance?
How does it compare to existing approaches?
How does it scale with increasing size of subject?

Datasets

How does the `maxE` minimum run length affect performance?

How does it compare to existing approaches?

How does it scale with increasing size of subject?

Conclusion

Augmented Interval Lists add the maximum running end value to a list of intervals
The data structure is simpler than other methods
AILists improve performance, particularly in highly contained interval sets